

�ϥμҺ�术�����ӭ���术结�G

 �U飞���X�x�ߴN�O��闭�ʸs论��Q��应�ΤT: �J�M�`杂现�H��为简单绕�骺�ۭ��A�Ө䤤�Y�@简单现�H��360个�����~观�A则��们�u��观��这�@现�H���䤤�@个�~观�C�Ҧp�Y现�H对�_(x,y)�����U��V�O�������A则��们�u�ݪu��X轴��观��现�H变�ơA简�ƤF观��C
�U飞���X�x�ߴN�O��闭�ʸs论��Q��应�ΤT: �J�M�`杂现�H��为简单绕�骺�ۭ��A�Ө䤤�Y�@简单现�H��360个�����~观�A则��们�u��观��这�@现�H���䤤�@个�~观�C�Ҧp�Y现�H对�_(x,y)�����U��V�O�������A则��们�u�ݪu��X轴��观��现�H变�ơA简�ƤF观��C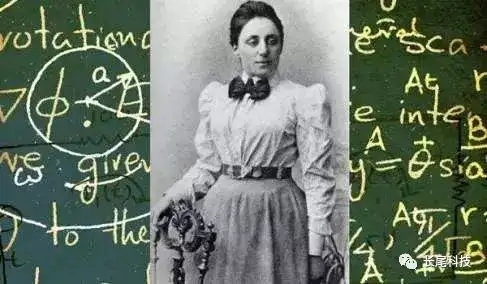



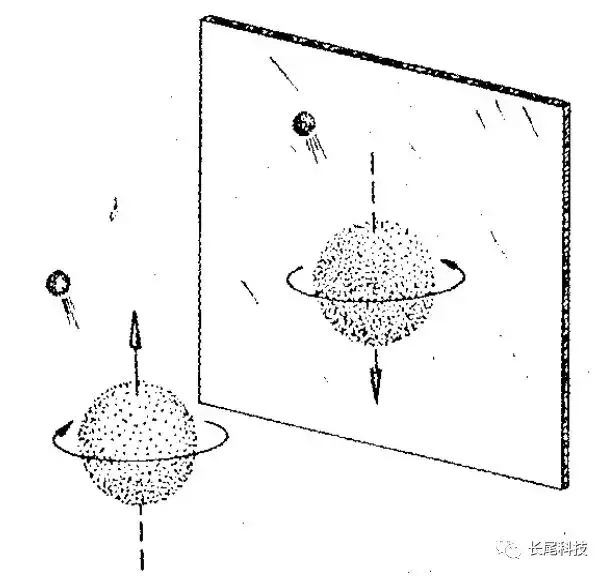 ��们�]�ܮe���Q�H�A镜�l���~����l�ֱ�转��V虽�M�ۤϡA���O�p�G�~����电�l���W飞�A镜�l������电�l�]���W飞�A这�ܲŦX�`识�A没���\�_�Ǫ��A这�N�O�t称�u��时�Ԫ����l�C���O�A�p�G���ѧA�ݨ�镜�l��电�l�~�M�O�¤U发�g���A�A会��会觉�o见���F�H
��们�]�ܮe���Q�H�A镜�l���~����l�ֱ�转��V虽�M�ۤϡA���O�p�G�~����电�l���W飞�A镜�l������电�l�]���W飞�A这�ܲŦX�`识�A没���\�_�Ǫ��A这�N�O�t称�u��时�Ԫ����l�C���O�A�p�G���ѧA�ݨ�镜�l��电�l�~�M�O�¤U发�g���A�A会��会觉�o见���F�H



 �W图�O�����对论���ޤO场��{�A�A�i诉��这���`杂����{�n����从实验数�u���h���X����来�H�G�B�A�����对论�b��们��`�ͬ������顿�ޤO��结�G�L�G�@���A�Ĩ�观测�F���\�h�Ѥ�数�u�i�H让开���ǩM��顿�h�q�����A���O�b20�@纪�즳ԣ数�u让�A�h�q�����对论�H���P���点进动问题�O���数���ŦX��顿�ޤO�z论���A���O�H们��对这��问题�A���M�Ĥ@��应�O�b���P����还���@颗�|��发现���p��P�A�Ӥ��O�ΤF�L�ʦ~����顿�ޤO��问题�C�h�@�E�B说�A�N��A当时认为���O�]为��顿�ޤO���{���̳y�����A���O�N这���@个数�u�A�A��\�i��从��归纳�X�����对论��场��{�H
�W图�O�����对论���ޤO场��{�A�A�i诉��这���`杂����{�n����从实验数�u���h���X����来�H�G�B�A�����对论�b��们��`�ͬ������顿�ޤO��结�G�L�G�@���A�Ĩ�观测�F���\�h�Ѥ�数�u�i�H让开���ǩM��顿�h�q�����A���O�b20�@纪�즳ԣ数�u让�A�h�q�����对论�H���P���点进动问题�O���数���ŦX��顿�ޤO�z论���A���O�H们��对这��问题�A���M�Ĥ@��应�O�b���P����还���@颗�|��发现���p��P�A�Ӥ��O�ΤF�L�ʦ~����顿�ޤO��问题�C�h�@�E�B说�A�N��A当时认为���O�]为��顿�ޤO���{���̳y�����A���O�N这���@个数�u�A�A��\�i��从��归纳�X�����对论��场��{�H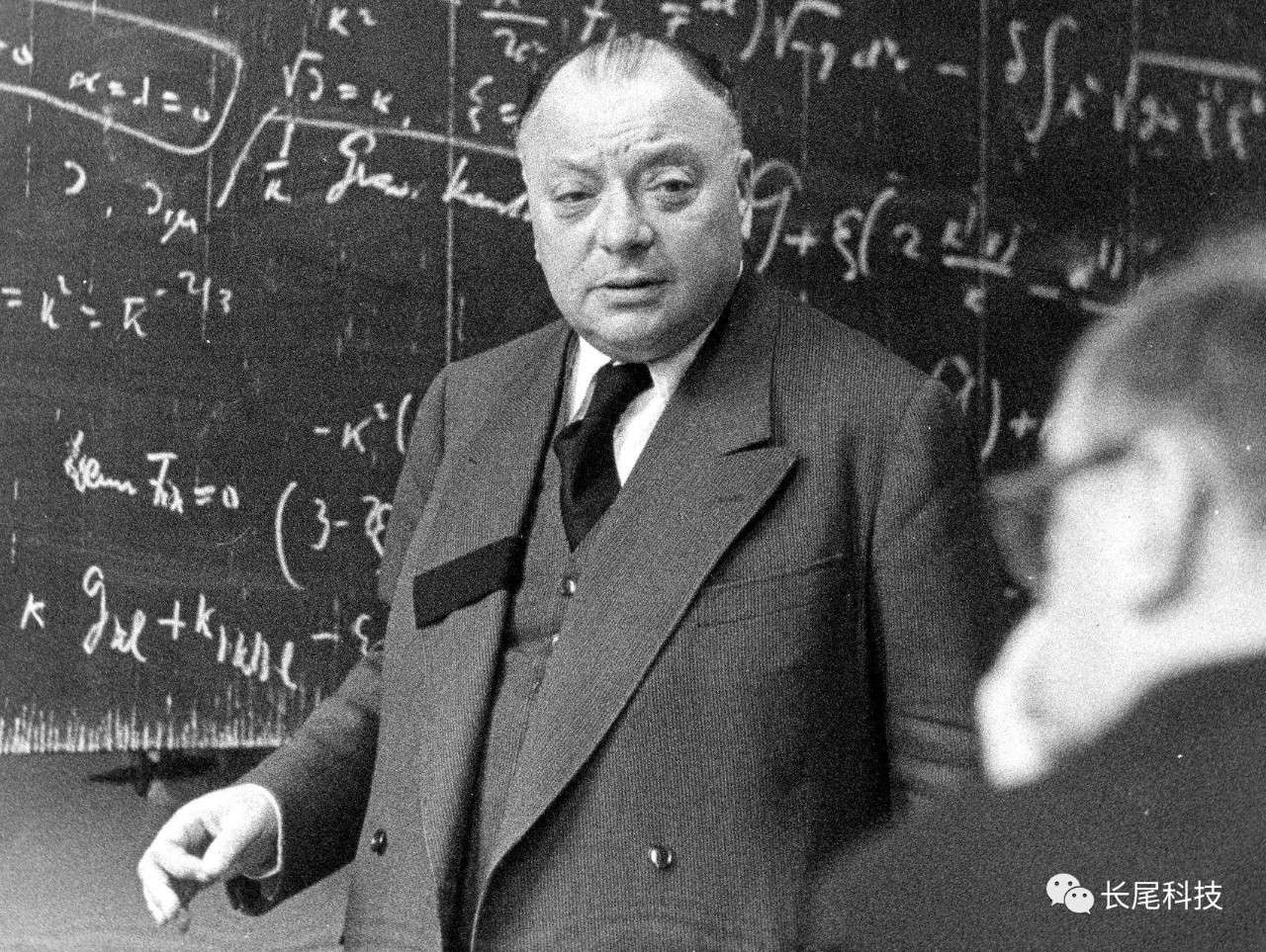

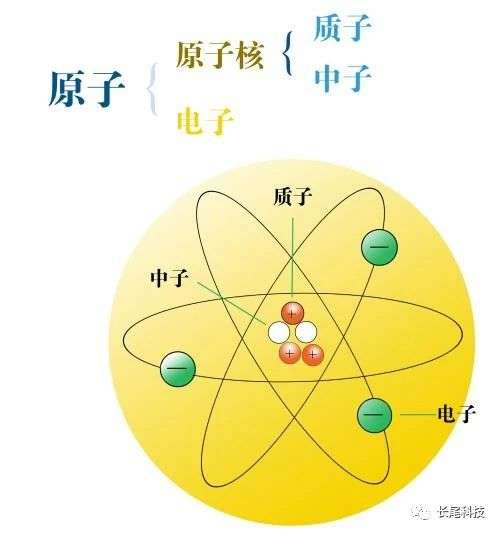 �_�O�A���˳��N来�F���X�F�@个�j胆���Q�k�G�L认为质�l�M���l压�ڴN�O�P�@���ɤl-�֤l��两�����P��状态�A��们�@�P组���F�@个�P��ۤG��态�C�b��H���P��۪�间���A质�l�i�H����转����为���l�A���l�]�i�H����转����为质�l�A�]为质�l�M���l�b�L�ۤ��@�ΤU�O�@�����A�ҥH�A��们�N�i�H说�G�L�ۤ��@�Ψ㦳�P��۪�间�U����转��变�ʡC
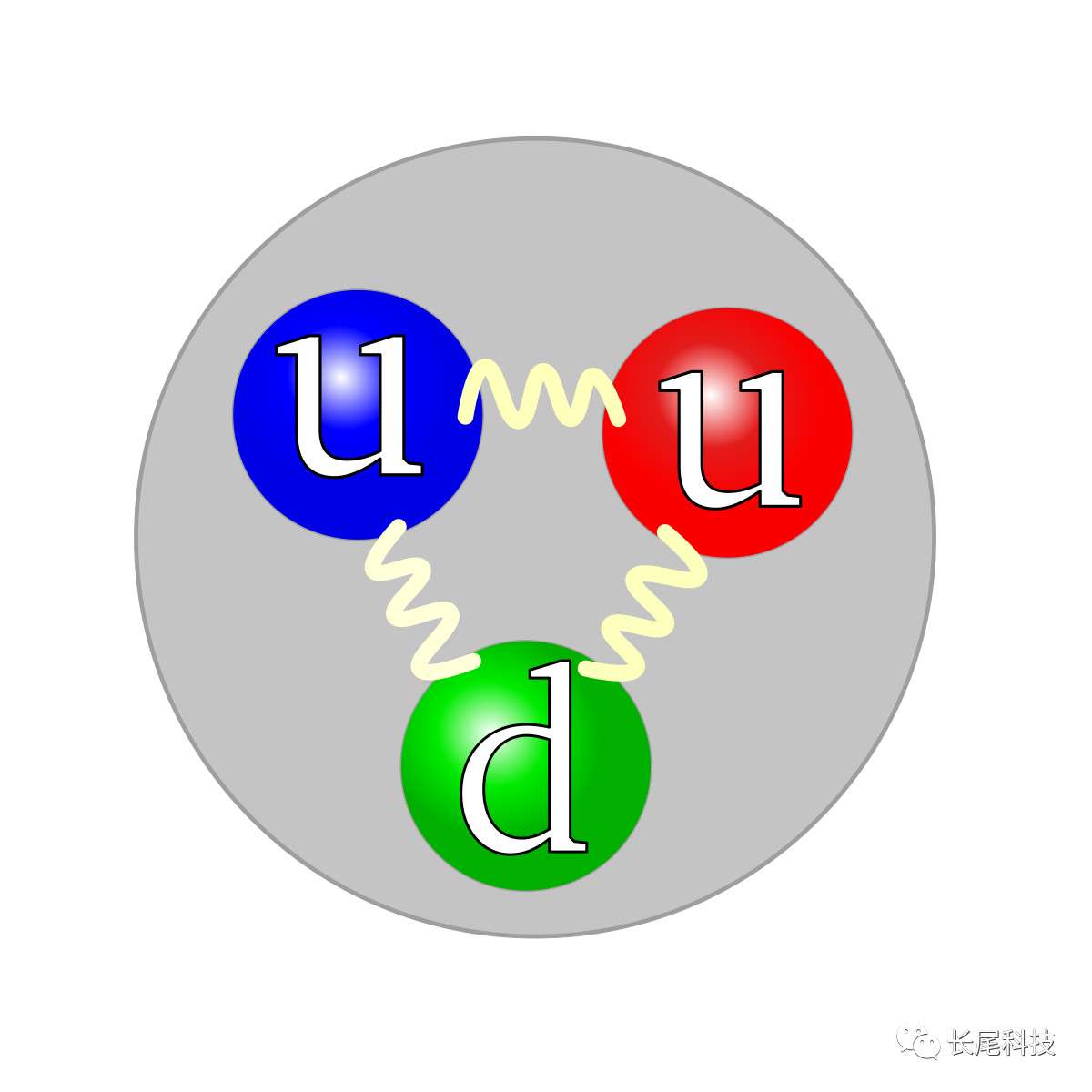
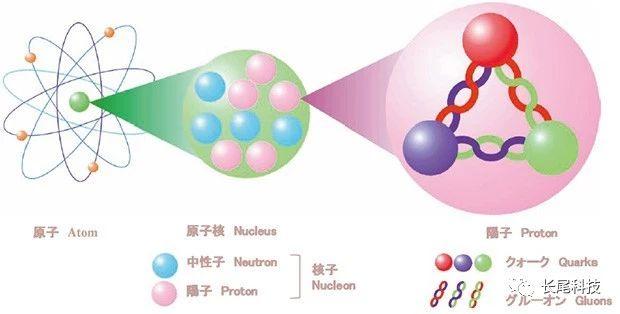
�_�O�A���˳��N来�F���X�F�@个�j胆���Q�k�G�L认为质�l�M���l压�ڴN�O�P�@���ɤl-�֤l��两�����P��状态�A��们�@�P组���F�@个�P��ۤG��态�C�b��H���P��۪�间���A质�l�i�H����转����为���l�A���l�]�i�H����转����为质�l�A�]为质�l�M���l�b�L�ۤ��@�ΤU�O�@�����A�ҥH�A��们�N�i�H说�G�L�ۤ��@�Ψ㦳�P��۪�间�U����转��变�ʡC ��简单���Ҥl�N�O��数���[�k�A�p学�ͳ����D�[�k满����换�ߡG3+5=5+3�A��论�A�[数��顺�ǫ�\��换�A�̦Z��结�G����变�C�_�O�A��们�N说��数�M��数���[�k�ۦ��F�@个��数�[�k�s�A这个�s��运��]�[�k�^�O满����换�ߪ��A�ҥH这个��数�[�k�s�N�O��贝�ظs�C
��简单���Ҥl�N�O��数���[�k�A�p学�ͳ����D�[�k满����换�ߡG3+5=5+3�A��论�A�[数��顺�ǫ�\��换�A�̦Z��结�G����变�C�_�O�A��们�N说��数�M��数���[�k�ۦ��F�@个��数�[�k�s�A这个�s��运��]�[�k�^�O满����换�ߪ��A�ҥH这个��数�[�k�s�N�O��贝�ظs�C





 |
�ϥμҺ�术�����ӭ���术结�G |
 |
 |
�����e2000�~�A�j�ڤ�伦�H�b�@���@����{时产�ͤF��数�A�Y���z数�F数�ʦ~�Z�A�L们�w�F�ѤF�G����{���ڦ��ѡA产�ͤF�Ӳz数�F16�@纪�A�N�j�Q数学�aCardano�MBombelli�b�D�Ѥ@���T����{时发���F虚数�C�ۦW数学�aSir Michael Atiyah(1929-2019)��h说�A虚数 [����] �O数学�v��伟�j��单个发���F�������_4�����h项����{�O�_�s�b�D�ڤ����A�ʥͤF�s论�C�D��线�ʤ�{组���|�F线�ʥN数�F
�]�]���A�`数�M线�N���O�s论内��结���ۦP�A联�t紧�K�C
�s论��诞�ͬO�N数�B�L��M数论�T个领�쪺发�i�@�P��动���C
1800�~���k�A�H们�w经会��1��4����{�A��对�_�D�ѧ�������{还没��头绪�C为�F�^��这个问题�A����数学�a��贝��(Niels Henrik Abel�A1802-1829)��贡�Y�}�h�A�䤤�̵ۦW���O����证���F5����{没���D�ڤ����C
�k国数学�a��罗��(Évariste Galois�A1811-1832�^进��s论��开创�ʤu�@�C�N数�w�z�i诉��们�G��{�O�L����N对应�L个�ڡA�s论���Ѥ@��证���N数�w�z����k�C
�t���h�P时(1798)�A����(Carl Friedrich Gauss, 1777-1855)�b��经�媺数论�ۧ@�����X�F�Һ�术(Modular Arithmetic)�A��逻辑�]�O�s�@�P�C�U图���A时钟����数为12�A [����] �C时钟����数为12
1800�~�N�A�w统�v�F两�d�~��欧�L���o�L��临���R�A双���L��M�y���L�D欧�L��I�����X�C�H们�ܧ�发现�s�O��s这�ǤL���n�u��A1827�~�A����乌��(August Ferdinand Möbius, 1790-1868)�b�������F�Ѹs�����������G�U�A�ϥίS�w�s���L��变��这�@��实对�L��
moon moon, [12/17/2021 4:55 AM]---------------------------
�G维�����A���h边�Υi�H����数��
�T维��间���h���^�A�ҥu��5���A��数学证�����@
�|维��维��维��间���������h���^�A�N���O�u��两��
��别�O��纬锥�ΩM�����^��纬扩�i��
��穷�h�A5�A2�A2�A2�K�K
�����实��仅仅�O���������A�ӬO�b�����^�t�����@个���M�q�Ϊ��@个东��
3�� 4�� 8�� 12�� 20��
给这�������h���^�t����A应该��\�t�O
�����实��仅仅�O���������A�ӬO�b�����^�t�����@个���M�q�Ϊ��@个东��
�b�U门学�쪺�̰�层�A����줭
��实�A�ܦh�a�賣�^现�X�`数5来
��p���_5������{没���ڦ��q��
这����话�A��{�]�i�H�t�W�����
�ڪ��P觉�a�A�����^结�X�ʳ̦n�A�N�t�b�̤��ߪ��g
欧�Ԥ���
这个���l���A��个数�r�A�]�i�H�t�W����
还�A�Ψ�F3��运��k则�A
5�O3�A�P时�X现�b�@个���l��
还���@个=号
�n�F�A这�N�O1�A3�A5齐���F
孙���Ū����T��13500��
moon moon, [12/17/2021 5:23 AM]
��p�ڡA给�@个数�r������A�L��������A虚数���������\���O�H为���\�s�b这����运��q�D�O�H�t�z为���\�n这���w�ƩO
moon moon, [12/17/2021 5:25 AM]
����A�^��A�Ӧ�A����
moon moon, [12/17/2021 5:27 AM]
�j�N������A��实�����O�i�H�t�b现�N��学����
moon moon, [12/17/2021 5:27 AM]
�z�Q�l�]来��
moon moon, [12/17/2021 5:30 AM]
还���A�P觉�a�A����}���O��5�������A����应该�O2^n这���������A5�O����+�k则�A
moon moon, [12/17/2021 5:31 AM]
��对�A��刚�~��个���l�A3+5=8�A这个�O5����+3�k则��
moon moon, [12/17/2021 5:33 AM]
5=1+2^2
moon moon, [12/17/2021 5:38 AM]
��A��这�~���M�ݥX来�A��个欧�Ԥ����A7个��号�A��2个��号�O隐�ê��A�~�M���n�t�_��C�P�M两颗隐�ê��P�P
moon moon, [12/17/2021 5:39 AM]
����M��号�A两个��号���O隐�ê�
moon moon, [12/17/2021 5:39 AM]
这�N���Ӫk则�O��质���۳q
moon moon, [12/17/2021 5:40 AM]
规���O���^�A�}�b�@个���l��
moon moon, [12/17/2021 5:40 AM]
��质�O�믫���ۤ��@��
moon moon, [12/17/2021 5:41 AM]
�ڴN�b�Q��\���t�O
�u��, [12/17/2021 5:48 AM]
师��这���@�ޥ�讲�A�N觉�o�O�E�����D���P觉�F�A
moon moon, [12/17/2021 5:50 AM]
�h���^欧�Ԥ����Gv - e + f = 2, �䤤v�O顶点�]vertex�^数�Ae�O边�]edge�^数�Af�O���]face�^数�C
moon moon, [12/17/2021 5:51 AM]
这����2�A
moon moon, [12/17/2021 5:51 AM]
�a��-�Ѥz���n�O2
moon moon, [12/17/2021 5:52 AM]
欧�Ԥ����t�W�_��P��话�A���\�_��P�O该�t�W���\�O�H
moon moon, [12/17/2021 5:52 AM]
�n��还�i�H���ӦA�t
moon moon, [12/17/2021 5:52 AM]
�t��h���P�P
moon moon, [12/17/2021 5:53 AM]
mv^n,�u�ڪ��A�u��mv动�q�Mmv^2 ��q�A
moon moon, [12/17/2021 5:55 AM]
�i满����换�ߪ�计��k则�A�u��两层�A�Ĥ@层+-�A�ĤG层�����A�ĤT层���誺�N�����换顺�ǤF
moon moon, [12/17/2021 5:56 AM]
��维��间���h���^�A�u��2��
moon moon, [12/17/2021 5:58 AM]
�E�k�ߤߩҳy�A�a����风���O�p来��
moon moon, [12/17/2021 5:59 AM]
认识�t�z�k则���P时�N�]�O�b认识�ۤv
�p�|, [12/17/2021 5:59 AM]
�E���E�����O���Ǫ�组���t变�A�t�z终��u�z�b����
moon moon, [12/17/2021 6:00 AM]
�_�O�A�V�~�D�J�O�V内��A两�̫D�@�D��
moon moon, [12/17/2021 6:03 AM]
�h���数学�����U���`数
moon moon, [12/17/2021 6:04 AM]
�S别�O�O进����关���A�b����进��U����须�n�O��个数���`数�C
moon moon, [12/17/2021 6:04 AM]
[In reply to �u��]
这个�s���A�t�z������对应
moon moon, [12/17/2021 6:05 AM]
�R盘�t�W�P�P
moon moon, [12/17/2021 6:05 AM]
�]�O�P�������
moon moon, [12/17/2021 6:07 AM]
�ڴN�Q�ڡA����数学�e�R�k
�u��, [12/17/2021 6:09 AM]
[In reply to moon moon]
这个��实�����i�H���@�A���@��H谁�Q��O�A师���u厉�`��F
moon moon, [12/17/2021 6:24 AM]
�O这����
moon moon, [12/17/2021 6:24 AM]
�n����Y�ܦh时�Գ���½译�O
��, [12/17/2021 6:30 AM]
师���A�z说��镇�T�ɡA��们�Τ��\�ͩR��镇�T�ɰڡA�{�I������
moon moon, [12/17/2021 6:32 AM]
[In reply to ��]
���h���覡�O
moon moon, [12/17/2021 6:32 AM]
�]�A���@�w亲�ۦb�T�ɨ����覡
moon moon, [12/17/2021 7:09 AM]
��y�z�A�����对应关�t�A数学�����O�������y�z�ڡA当�M�O�@个对应�^�t�A��{��对应�^�t�C���\ �E宫�������N�]�O�@个对应�^�t�C
moon moon, [12/17/2021 7:10 AM]
还����L��对应�^�t�A��p��16宫
�u护���, [12/17/2021 7:14 AM]
��N�O���P对应�^�t �^现���O���P���k则
moon moon, [12/17/2021 7:15 AM]
��h���A��p�~应
moon moon, [12/17/2021 7:15 AM]
谁说�V�~�䤣��吗�A�s�e�j�a�A尽�O���ߩ�现
moon moon, [12/17/2021 7:16 AM]
�@�y话�A�N�O牵�L��会�A�v风�N�O�B
�u��, [12/17/2021 7:17 AM]
�@对�~应�]�O�A�O���A���O��
moon moon, [12/17/2021 7:17 AM]
这�N�s��������维�A�W�V����
moon moon, [12/17/2021 7:17 AM]
逻辑
�u��, [12/17/2021 7:19 AM]
��߷P���ȧ��A远远�W�V�z��逻辑�A�餼�����F ��觉
�u护���, [12/17/2021 7:19 AM]
没���k则���k则
moon moon, [12/17/2021 7:19 AM]
数学�y�z�O�@个����对应关�t�A�C个��{�A��问题转�ƨ�数学�^�t������
moon moon, [12/17/2021 7:20 AM]
�e�R��实�O�@个�����M�g过�{�A
moon moon, [12/17/2021 7:20 AM]
�Ӧ۵M�ɡA�����N�P�B进����这��
�u��, [12/17/2021 7:23 AM]
�P�B进���ӡA�j�۵M�O�p����备�A�ܥȦܪ�
moon moon, [12/17/2021 7:25 AM]
�N����L��问题转�ƨ짤标�t�N数问题�W�h�A这���ѪR�L��N�O�@��标�㪺�e�R过�{�C
moon moon, [12/17/2021 7:25 AM]
����对应关�t��实没���\�z�ѡA
moon moon, [12/17/2021 7:26 AM]
�u�n�i�H�إ߰_来�@�@对应�A�N�i�H这��转�ƤF
�u护���, [12/17/2021 7:27 AM]
��这�N�O����来�F�����P觉
�u护���, [12/17/2021 7:27 AM]
没���\�z��
moon moon, [12/17/2021 7:27 AM]
���\�A�ڴN���个��转�ƨ�E宫���A�Ѥz�a�䤤
moon moon, [12/17/2021 7:27 AM]
这个�]�O�P�����D历
moon moon, [12/17/2021 7:28 AM]
��阄��实�]�O�P�����D�z
moon moon, [12/17/2021 7:28 AM]
���O�e�R��过�{�A��对应点��过�{�C
moon moon, [12/17/2021 7:29 AM]
记�o�p学��应��题刚刚�Τ�{�h�Ѫ��P觉吗
moon moon, [12/17/2021 7:29 AM]
��\对应���{�W�N�i�H���\变来变�h�F�O�H
moon moon, [12/17/2021 7:30 AM]
纯�骺��数学�k则�A�I�Z��现实�k则�����Φ�虑�F
�u护���, [12/17/2021 7:30 AM]
����😄对对
moon moon, [12/17/2021 7:30 AM]
�N�O���F这个对应��间
moon moon, [12/17/2021 7:30 AM]
�N�����t�z��������换
moon moon, [12/17/2021 7:31 AM]
��时�����աA对
moon moon, [12/17/2021 7:31 AM]
�i�O�������ӡA�Ҥ]�i�H������对
�u��, [12/17/2021 7:31 AM]
���Ω��մN运��N�O�� �O��
moon moon, [12/17/2021 7:35 AM]
���\�ڴN�b�E宫�W���p�@�M运��k则
moon moon, [12/17/2021 7:35 AM]
�N��数学�k则�@���A
�u��, [12/17/2021 7:36 AM]
���O�A这�~�O�̺�m��
�p�| ���, [12/17/2021 7:41 AM]
�H���R运�Q�w��F�A�b�E宫���p�@�M运��k则�A�f�R��Ѫ�轨迹
�u��, [12/17/2021 7:43 AM]
�O�r��R��R
�u��, [12/17/2021 7:43 AM]
�کR�ѧڤ��ѡ��ѡ�
�p�|, [12/17/2021 7:45 AM]
�i�H�Q��A师��这��选择�b�ä��E运�e�X来�A�N�O�@场�j���E宫���p
moon moon, [12/17/2021 7:45 AM]
这个对应过�{�A��实�������i�H�Τ�来����
moon moon, [12/17/2021 7:46 AM]
�ߨ��Q�ӭ�个对应��个�N�O
�u��, [12/17/2021 7:48 AM]
[In reply to moon moon]
�p�N�C���ʡA���ڦ�
�u护���, [12/17/2021 7:53 AM]
�^师这����来���a势�M��仪�A�p���s�p�y���C�S�H�O�A�@双温�x���j���D�N�F�@�U�t�z�A带�ӥL�ӥi�ܩڪ���z�O�A让��个�t�z���p�착�訽��C个����ը��A�k�ӥi�k�C
�u��, [12/17/2021 7:53 AM]
绝对�P
�u��, [12/17/2021 7:54 AM]
[In reply to moon moon]
�N�ΧA��运��A���O�O�ڪ�规则�B��释权
�u��, [12/17/2021 7:56 AM]
�@个东��还�O�����A��内�b���变�F
moon moon, [12/17/2021 7:57 AM]
���p�U�����@�M�k则�A��实�O��来�ѵM�N�s�b��
moon moon, [12/17/2021 7:57 AM]
����p�N�s�b
�u��, [12/17/2021 7:58 AM]
��来�ѵM��
�p�|, [12/17/2021 7:58 AM]
润��细��声
�u��, [12/17/2021 8:02 AM]
润��细��声�A���x�Ӻ믫�C��来�F
�u��, [12/17/2021 8:03 AM]
�Q�K�l��来
�p�|, [12/17/2021 8:04 AM]
师����来讲���V来�V���A�}�F���Ъk轮�\�ܦh���G�ʦL
moon moon, [12/17/2021 8:13 AM]
���\�إߤF������对应关�t���Z�A���R运�A���盘�����A�N���F�R����
moon moon, [12/17/2021 8:13 AM]
�O�@��������对应关�t
moon moon, [12/17/2021 8:13 AM]
�n�{�I
moon moon, [12/17/2021 8:14 AM]
这���N�O���P������t�z��间�p��显�Ƴq�H���
�u��, [12/17/2021 8:26 AM]
[In reply to moon moon]
��镜�l沟�q
moon moon, [12/17/2021 8:17 AM]
����学���F�_门�P�ҡA�i�H��会盘����ڰ�
moon moon, [12/17/2021 8:36 AM]
(2, 7, 6, 9, 5, 1, 4, 3, 8)
(2, 9, 4, 7, 5, 3, 6, 1, 8)
(4, 3, 8, 9, 5, 1, 2, 7, 6)
(4, 9, 2, 3, 5, 7, 8, 1, 6)
(6, 1, 8, 7, 5, 3, 2, 9, 4)
(6, 7, 2, 1, 5, 9, 8, 3, 4)
(8, 1, 6, 3, 5, 7, 4, 9, 2)
(8, 3, 4, 1, 5, 9, 6, 7, 2)
moon moon, [12/17/2021 8:37 AM]
�E宫图�i�H��8���Φ���变��
moon moon, [12/17/2021 8:37 AM]
�p�G���n�D对��线�۵��A�i�H��72��
| �w����{ �u�ߤH (http://qingqing.freebbs.tw/) | Powered by Discuz! 5.0.0 |